COMMENT | We are right in the middle of the Covid-19 pandemic. As mathematicians, we are concerned about two major issues: (1) What is the prognosis for the current Covid-19?; and (2) How to stop a potential second wave?
During the 2009 H1N1 pandemic, we were equally worried about the possibility of a second wave (Koh and Teh, 2011) but fortunately, that did not happen.
The extension of the movement control order (MCO) by another two weeks to April 14, 2020, is absolutely necessary to prevent a potential immediate second wave.
So, we tried to use some simple calculus to demonstrate how mathematics can help to illuminate on two critical issues and help us prepare to confront the potential Covid-20.
To do this we need to have some quantitative capability to look at Covid-19 epidemic evolution with MCO in place. We need to understand the dynamics of infectious disease such as Covid-19.
The dynamic evolution of Covid-19 can be mathematically described by a system of differential equations known as the SIR (Susceptible-Infectious-Recovery) epidemic model.
For technical details, see Koh and Teh (2011). We are more than willing to share our experiences and simulation model known as FluSim@USM.
Here, we will summarise some of the mathematics involved.
Goal: R0 below 1.0
Epidemiology models have been successfully used to track and control Covid-19 in China recently. A key issue is to determine what can be done to force the outbreak to die out quickly.
The most important epidemic threshold is known as the basic reproduction number typically denoted by R0 (pronounced "R-naught" or "R-zero").
This reproduction number can be seen as how contagious the virus is. If R0 is less than 1.0, the outbreak will die out. On the other hand, if R0 is greater than 1.0, the outbreak will grow exponentially.
A protocol of effective control measures should, therefore, aim to quickly reduce R0 to less than 1.0, without disrupting social and economic order too much.
Unfortunately, R0 cannot be measured directly. So, some form of maths is needed to calculate this elusive number.
For the SIR model, the basic reproduction number is given by R0 = BT, where B is the contact rate and T is the mean infective period. The infective period T for Covid-19 is estimated to be about 11.5 days.
We, as the public, cannot change the infective period T. This is the property of Covid-19. But we certainly can cut down the contact rate B by strictly maintaining social distancing and other mitigating measures as ordered by MCO.
Other measures are equally important, such as aggressively isolating infected and infective persons, and effective contact tracing to find those who are infective.
The attached figure shows daily new infected persons from Jan 25 to March 30 provided by the Health Ministry. This data is crucial to calibrate and validate the SIR model.
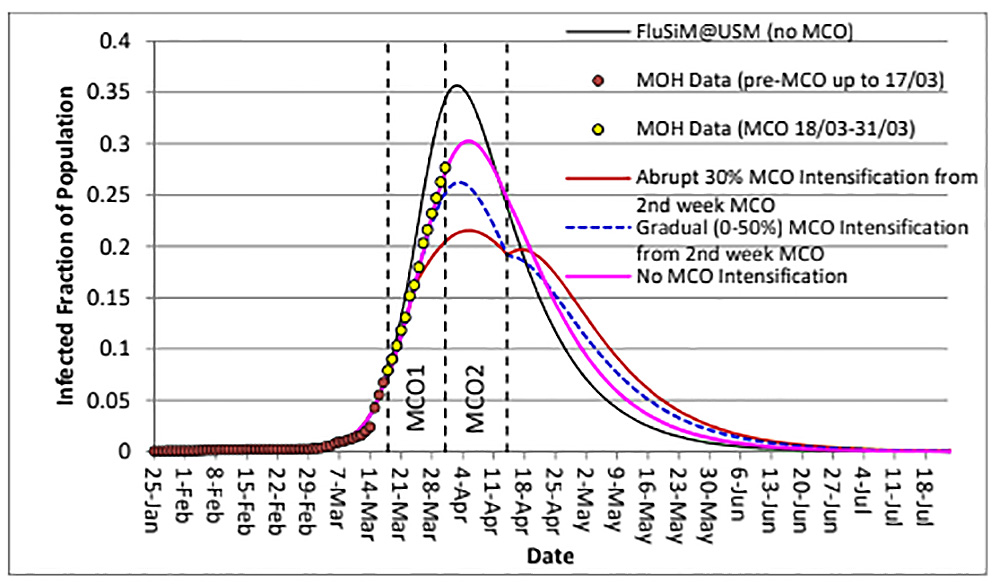
For the first phase from Jan 25 to March 1, the total number of infected persons is 22 and R0 was about 1.5, which is slightly higher than 1.0. Therefore Covid-19 infection started in Malaysia around Jan 25 and grew slowly.
But soon after March 01, R0 quickly skyrocketed to 3.5, pushing the infection to grow very quickly, with daily new infected persons rising by three digits. The first two weeks of MCO managed to reduce R0 to 2.95. However, this value is still much higher than 1.0.
Therefore, we must aggressively enforce the extended MCO. We must aggressively maintain social distancing, self-isolation, enforced-isolation, and containment of infected and infective persons. We urge everyone to take MCO very seriously with full compliance.
Take full personal responsibility to contain this horrible Covid-19. MCO measures are critical to the containment of Covid-19. And critical to the prevention of an immediate second wave.
Reference:
Koh, H.L. and Teh, S.Y. (2011). FluSiM Simulation for Malaysia: Towards Improved Pandemic Surveillance. International Journal of Chemical Engineering and Applications (IJCEA) 2(1), 53-59. ISSN: 2010-0221.
TEH SU YEAN and LUTFI AMRI RAMLI teach at the School of Mathematical Sciences, Universiti Sains Malaysia.
KOH HOCK LYE is a senior fellow at the Jeffrey Sachs Center on Sustainable Development, Sunway University.
The views expressed here are those of the author/contributor and do not necessarily represent the views of Malaysiakini.
Keep up with the latest information on the outbreak in the country with Malaysiakini's free Covid-19 tracker.
Malaysiakini is providing free access to the most important updates on the coronavirus pandemic. You can find them here.
Help keep independent media alive - subscribe to Malaysiakini.


